Like most parents in Singapore, we leave no chance to getting to the best schools for our children. My wife wants to move closer to Nanyang Primary to increase our chance of getting a place. I did not want to do that. Our chances are high enough that it doesn’t warrant such extremes. I realised I needed to prove my point.

How does primary school registration work?

For the uninitiated, primary school registration is broken up into phases - similar to a priority queue, where the earlier phases get the places first. Phase 1 is for siblings of current students. Phase 2A is for the alumni. Phase 2B is for parent volunteers, community leaders, anybody related to the school. Finally, Phase 2C is for the public. When there are more applicants than places, citizens are prioritised over foreigners, followed by those living near the school. Details on the official website

I’m lucky. I have two options. As an alumni of Nanyang Primary, I qualify for Phase 2A. As I live near Ai Tong School, I have a chance in Phase 2C. Both schools are wife-approved. What is the probability of my child getting into either schools?

Probability of getting into Nanyang Primary

The probability is dependent on 2 things: number of applicants and the number of places. The number of places depends on the number of applicants from Phase 1. How many will apply for Phase 1 in 2018?

Finding the number of places for Phase 2A

If you didn’t know already, the number of people who drowned by falling into a pool correlates to the films Nicholas Cage appeared in. We ought to treat correlation results with care. However, it makes sense that the birth rate should correlate to the number of applicants. I took the birth data from the published government statistics. The enrolment statistics and balloting statistics for Nanyang Primary are published as well.

The above is a table of data tabulating the number of resident births and Phase 1 applicants to Nanyang Primary. The correlation coefficient between the applicants and births is below.

The number of applicants is negatively correlated to the birth rate. Which means when there are more births, there are less applicants. It doesn’t make sense. Let’s look at the scatter plot.

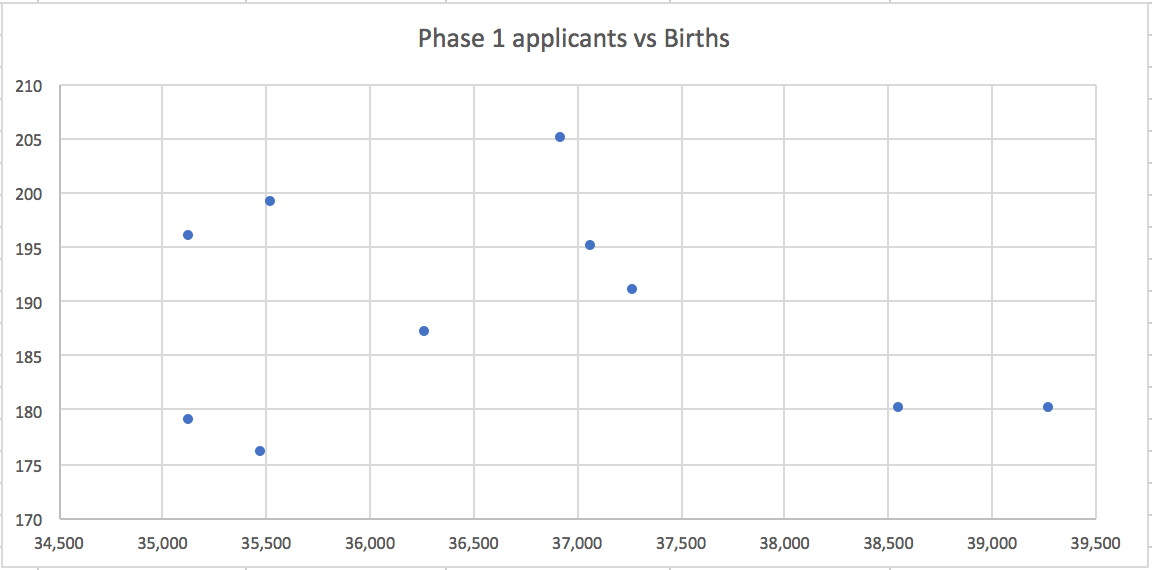
Applicants in 2018 will come from births in 2012 which is 38,641. To be conservative, I selected the three points on the top left, drew a line through them to interpolate the number of applicants for 2018. It is 215. Since the number of places at Nanyang is 390, that leaves

1

390 - 215 = 175

175 places. There is a law introduced in 2014 that there must be at least 40 places kept for Phase 2B and 2C. In the worst case scenario, that leaves

1

175 - 40 = 135

135 places for Phase 2A. We now know the number of places on offer. Let us find the number of applicants next.

Finding the number of applicants for Phase 2A

Likewise, I believe that the number of applicants for Phase 2A should correlate to the number of births.

Likewise, we tabulate the number of resident to Phase 2A applicants. The correlation coefficient between the applicants and births is below.

Again we see negative correlation, which does not make sense. It is likely to be skewed by the data from 2007-2008. Let’s use the scatter plot instead.

Ignoring the 2 data points from 2007-2008(at bottom right), I draw a line through to interpolate the number of applicants for Phase 2A. I arrived at 145 applicants.

With this figure, we can calculate the probability of my child getting a place in Nanyang Primary in Phase 2A.

1
2
3

Probability = (Number of places) / (Number of applicants in Phase 2A)
 = 135 / 145
 = 0.931034483

My daughter has a 93.1% chance of getting into Nanyang Primary. That’s reassuring.

Backup plan: Ai Tong

In the 6.9% chance that my daughter won’t get into Nanyang Primary, what is the probability of her entering Ai Tong? That is dependent on the number of applicants to the number of places. Since the ruling in 2014 ensures that there are at least 20 places for Phase 2C, let us assume the worst and use 20 for the number of places available.

Finding the number of applicants for Phase 2C

Consistent with what we did previously, the number of Phase 2C applicants should correlate to the number of births.

There is data published on Kiasu Parents. The figures are in percentages. I had to infer the places from the percentages. TUR stands for cumulative take up rate, which is the percentage of the places that were taken by Phase 2C. APP is the ratio of applicants to the places available. As we are assuming the worst, we are not using that to estimate the number of places.

If we correlate births to the number of applicants, it returns a negative value which does not make sense. If we correlate number of applicants to the places available, it returns a positive correlation of around 0.55. Parents could be making their decision to apply based on the number of places available.

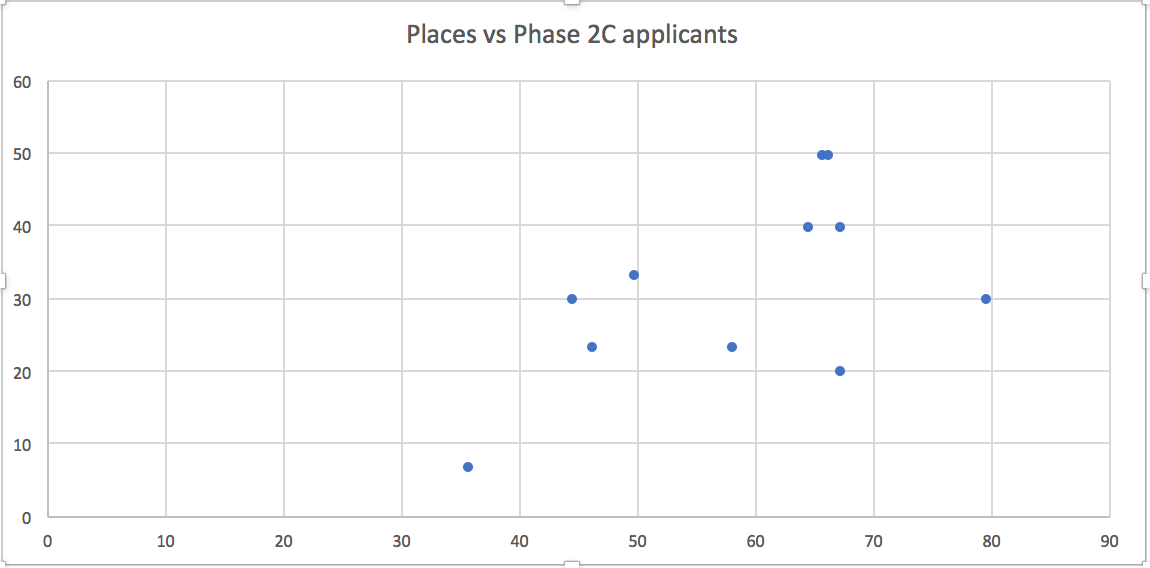
Using the scatter plot, I drew a line to interpolate the number of applicants given 20 places. It is 42.

1
2
3

Probability = (Number of places) / (Number of applicants in Phase 2C)
 = 20 / 42
 = 0.476190476

We conclude that my daughter has a 47.6% chance of getting into Ai Tong at Phase 2C.

Bringing everything together

I have both the probabilities for getting a place in Nanyang Primary and Ai Tong. What I want to know is the probability of getting into either.

Let us first define our terms.

1
2
3
4

A is the probability that we get a place in Nanyang
B is the probability that we get a place in Ai Tong
C is the probability that we get a place in Ai Tong, given we failed to get a place in Nanyang
D is the probability that we failed to get a place in Nanyang

To help the reader, I’ve copied out some probability equations.

1
2
3
4
5

P(A|B) = P(A n B) / P(B) # conditional probability
P(A n B) = P(A) * P(B|A) # when both A and B occurs
P(A n B) = P(A) * P(B)   # for independent events
P(A n B) = 0             # for mutually exclusive events
P(A u B) = P(A) + P(B) - P(A n B)

We want the result of the probabilities of A and C together. Since A anc C are mutually exclusive, P(A n C) is 0. The final result would be the addition of both probabilities.

1
2
3

P(A u C) = P(A) + P(C) - P(A n C)
         = P(A) + P(C) - 0
         = P(A) + P(C)

We already know P(A) = 0.931. So we need to find P(C). Let us define P(C) as a conditional probability, since we want the probability of getting into Ai Tong, given that we failed to get a place in Nanyang.

1
2

P(C) = P(B|D)
     = P(B n D) / P(D)

Does getting a place in Nanyang affect the probability of getting a place in Ai Tong? The number of places don’t change as it is set by law. The number of applicants will still be the same as people applying do not care about my result. They are mutually exclusive. Therefore,

1

P(B n D) = 0

Which means

1
2
3

P(C) = P(B|D)
     = P(B n D) / P(D)
     = 0

That is obviously wrong. Did we do something wrong? Let’s redefine C as the probability that we get a place in Ai Tong, and we failed to get a place in Nanyang.

1
2

P(C) = P(B n D)
     = P(B) * P(D)

We plug the result back to our first equation.

1
2
3
4

P(A u C) = P(A) + P(C)
         = P(A) + (P(B) * P(D))
         = 0.931 + (0.476 * 0.069)
         = 0.963844

It means that my daughter has an increased chance of 96.3% of getting into Nanyang or Ai Tong. That’s reassuring.

With that figure, I can tell my wife not to worry. With this simple episode, you can see the usefulness of Math in helping to make decisions. Intuition can be misleading. We must demand rigour in thinking when making decisions that has big impact.